Prolongation of a diffeomorphism
Consider a diffeomorphism of the total space of a smooth vector bundle $E$
$$ \varphi: E \to E $$We can define a transformation $\varphi^{(k)}:J^kE \to J^kE$ following the same ideas as below .
Prolongation of a group action
[Olver 1986] page 98
Suppose a group $G$ acting on a the total space of a smooth vector bundle
$$ \pi: E \rightarrow M $$We are going to define a new action on the jet bundle.
Let $g\in G$, $g: E\rightarrow E$. Then we define
$$ pr^n g: J^n(E)\rightarrow J^n(E) $$in the following way. Consider $P=[s]_x^n\in J^n(E)$ and $p=\pi_0(P)=s(x)\in E$ (see here the definition of $\pi_1$).
Suppose we can shrink the domain of $s$ to $U\subseteq M$ in such a way that the set $g(s(U))$ is the image of another section $\widetilde{s}$ (that is, $\widetilde{s}(\widetilde{U})=g(s(U))$) and denote $\widetilde{x}=\pi(g\cdot p)$. Then we define
$$ pr^n g(P)=[\widetilde{s}]_{\widetilde{x}}^n $$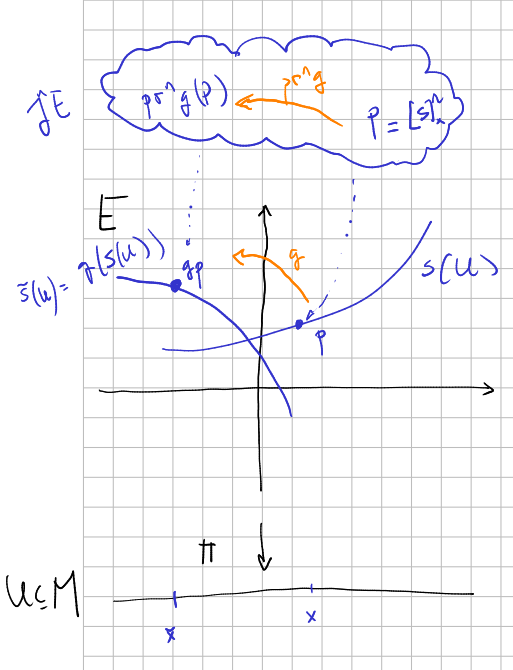
In coordinates
Anco_2002 page 62. I think is BETTER in xournal_041. Also in Mansfield_2010 page 32.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: